Ángulos: Agudo, Recto y Obtuso 1848479 | Celenia Nathalí inicia este fascinante recorrido, brindando a los lectores una perspectiva detallada y objetiva sobre este tema, cautivando desde el principio con su originalidad.
En este artículo, exploraremos los diferentes tipos de ángulos, aprenderemos a medirlos y comprenderemos sus propiedades. Además, descubriremos aplicaciones prácticas de los ángulos en diversos campos, ampliando nuestra comprensión de este concepto fundamental.
Tipos de ángulos
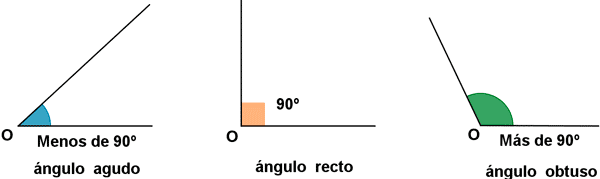
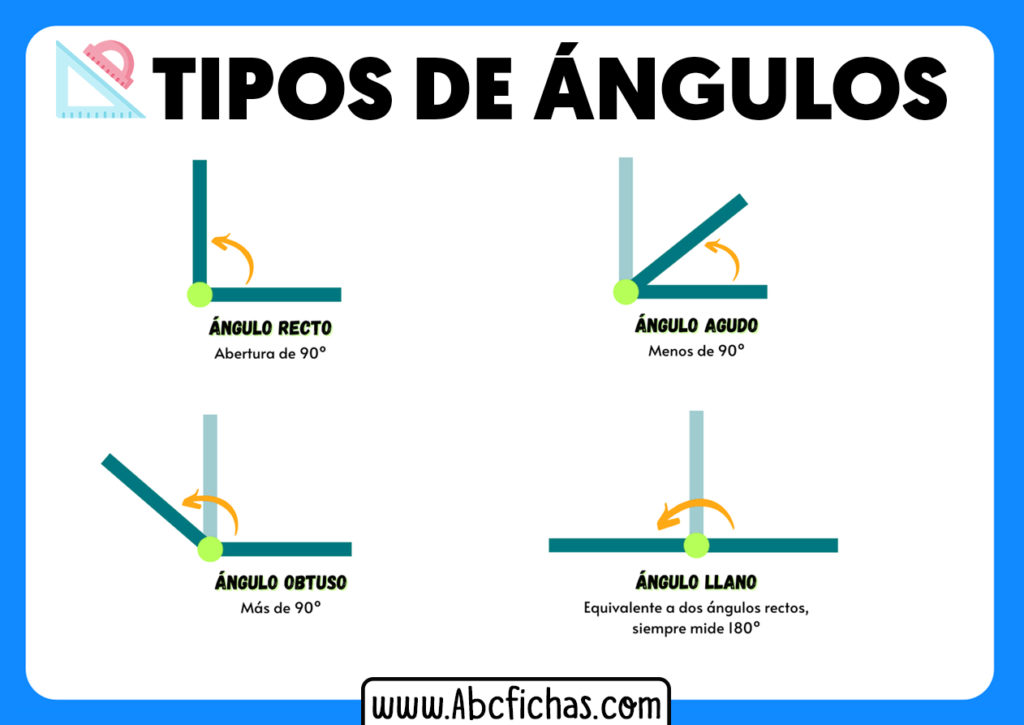
Los ángulos son figuras geométricas formadas por dos rayos que comparten un punto final común llamado vértice. Según su medida, los ángulos se clasifican en tres tipos: agudos, rectos y obtusos.
Ángulos agudos
Los ángulos agudos son aquellos que miden menos de 90 grados. Se caracterizan por ser menores que un ángulo recto. Por ejemplo, un ángulo de 60 grados es un ángulo agudo.
Ángulos rectos

Los ángulos rectos miden exactamente 90 grados. Son ángulos que forman una esquina cuadrada. Por ejemplo, el ángulo formado por las dos paredes de una habitación es un ángulo recto.
Ángulos obtusos
Los ángulos obtusos son aquellos que miden más de 90 grados pero menos de 180 grados. Son ángulos mayores que un ángulo recto pero menores que un ángulo llano. Por ejemplo, un ángulo de 120 grados es un ángulo obtuso.
Medición de ángulos
La medición de ángulos es un aspecto fundamental en geometría. Permite cuantificar el tamaño de los ángulos y determinar sus relaciones. Existen diversos métodos para medir ángulos, cada uno con sus ventajas y aplicaciones específicas.
Uso del transportador
El transportador es un instrumento comúnmente utilizado para medir ángulos. Es un semicírculo graduado con marcas que indican los grados. Para medir un ángulo con un transportador, se deben seguir los siguientes pasos:
- Colocar el centro del transportador en el vértice del ángulo.
- Alinear la línea base del transportador con uno de los lados del ángulo.
- Leer la marca en el transportador que se encuentra sobre el otro lado del ángulo.
Otros instrumentos
Además del transportador, existen otros instrumentos utilizados para medir ángulos, como:
- Goniómetro: Un instrumento de precisión utilizado para medir ángulos con gran precisión.
- Teodolito: Un instrumento topográfico utilizado para medir ángulos horizontales y verticales.
- Clinómetro: Un instrumento utilizado para medir ángulos de inclinación.
Pasos detallados para medir ángulos con precisión, Ángulos: Agudo, Recto Y Obtuso 1848479 | Celenia Nathalí

Para garantizar mediciones precisas, es importante seguir los siguientes pasos:
- Utilizar un instrumento adecuado para el tipo de ángulo que se está midiendo.
- Colocar el instrumento correctamente en el vértice del ángulo.
- Leer la medida del ángulo con cuidado y precisión.
- Repetir la medición varias veces para confirmar su exactitud.
Propiedades de los ángulos
Los ángulos tienen propiedades específicas que permiten clasificarlos y determinar sus relaciones. Estas propiedades incluyen:
- Ángulos adyacentes: Son dos ángulos que comparten un lado común y tienen un vértice en común. La suma de los ángulos adyacentes es igual a 180 grados.
- Ángulos complementarios: Son dos ángulos cuya suma es igual a 90 grados.
- Ángulos suplementarios: Son dos ángulos cuya suma es igual a 180 grados.
Ángulos adyacentes
Los ángulos adyacentes son fáciles de identificar ya que comparten un lado y un vértice. La siguiente imagen muestra dos ángulos adyacentes, donde el lado común es la línea AB y el vértice común es el punto A:
Ángulos complementarios
Los ángulos complementarios son aquellos que forman un ángulo recto, es decir, suman 90 grados. Por ejemplo, si un ángulo mide 30 grados, su ángulo complementario medirá 60 grados.
Ángulos suplementarios
Los ángulos suplementarios son aquellos que forman una línea recta, es decir, suman 180 grados. Por ejemplo, si un ángulo mide 120 grados, su ángulo suplementario medirá 60 grados. Comprender estas propiedades es esencial para resolver problemas relacionados con ángulos y para comprender conceptos geométricos más avanzados.
Aplicaciones de los ángulos en la vida real: Ángulos: Agudo, Recto Y Obtuso 1848479 | Celenia Nathalí
Los ángulos son conceptos geométricos esenciales que encuentran aplicaciones prácticas en diversas áreas de la vida real. Su comprensión juega un papel crucial en la resolución de problemas y el diseño de soluciones eficientes.
Arquitectura
En arquitectura, los ángulos determinan la forma, estabilidad y estética de los edificios. Los arquitectos utilizan ángulos agudos para crear techos inclinados que permiten que el agua de lluvia se escurra fácilmente. Los ángulos rectos se emplean para crear estructuras estables y simétricas, mientras que los ángulos obtusos pueden agregar interés visual y dinamismo a los diseños.
Ingeniería

En ingeniería, los ángulos son cruciales para diseñar puentes, máquinas y otras estructuras. Los ingenieros utilizan ángulos para calcular las fuerzas y tensiones que actúan sobre las estructuras, asegurando su estabilidad y seguridad. Por ejemplo, en el diseño de puentes, los ángulos de los pilares y cables juegan un papel vital en la distribución de cargas y la prevención del colapso.
Diseño
En diseño, los ángulos se utilizan para crear composiciones visuales agradables y funcionales. Los diseñadores utilizan ángulos agudos para atraer la atención, ángulos rectos para crear equilibrio y ángulos obtusos para añadir profundidad y contraste. La comprensión de los ángulos ayuda a los diseñadores a guiar la mirada del espectador y crear diseños que sean tanto estéticamente agradables como fáciles de usar.
